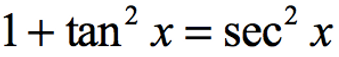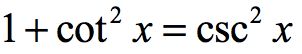CSET 3 REVIEW
Calculus (22 Multiple Choice Items, 3 Constructed Response Items)
Trigonometry
a. Prove that the Pythagorean Theorem is equivalent to the trigonometric identity and that \
this identity leads to and .
Lesson 1. Proof of Pythagorean Theorems: https://www.youtube.com/watch?v=iEKT-yAuRgQ; https://www.youtube.com/watch?v=MyO2MFJbfi4
b. Prove and apply the sine, cosine, and tangent sum formulas for all real values.
Lesson 2. Proof of Sin Sum Formula: https://www.youtube.com/watch?v=R0EQg9vgbQw
Lesson 3. Visual Proof of Sine and Cos Sum Formulas: https://www.youtube.com/watch?v=ea6-ctMYn_Q
Lesson 4. Proof of Cos Sum Formula: https://www.youtube.com/watch?v=gDOGT6NcD60
Lesson 5. Proof of Tan Sum Formula: https://www.youtube.com/watch?v=1qCXck4ZIrk
c. Analyze properties of trigonometric functions in a variety of ways (e.g., graphing and solving problems, using the unit circle)
Lesson 6. Properties of Trig Functions: https://www.youtube.com/watch?v=ypenWNeRdd4; https://www.youtube.com/watch?v=r26NNufSFYg; https://www.youtube.com/watch?v=soIt2TwV6Xk; https://www.youtube.com/watch?v=8Z60_yXX4xA; https://www.youtube.com/watch?v=ztlVm6COcK4; https://www.youtube.com/watch?v=Dis8_Ih7slo; https://www.youtube.com/watch?v=ZffZvSH285c
Lesson 7. Evaluating Trig Functions: https://www.youtube.com/watch?v=8DdyCeTEGOo; https://www.youtube.com/watch?v=QukM0eBDwNE; https://www.youtube.com/watch?v=9OdJ54fGgVs
Lesson 8. Symmetry of Trig Values: https://www.youtube.com/watch?v=tzQ7arA917E
Lesson 9. Use Trig Identities to Evaluate Expressions: https://www.youtube.com/watch?v=sGDbKmWmTDw
d. Apply the definitions and properties of inverse trigonometric functions (i.e., arcsin, arccos, and arctan)
Lesson 10. Introduction: https://www.youtube.com/watch?v=bBBUMHe900U; https://www.youtube.com/watch?v=JGU74wbZMLg; https://www.youtube.com/watch?v=hxjmtDXXCzU; https://www.youtube.com/watch?v=Idxeo49szW0
Lesson 11. Evaluating Inverse Trig Functions: https://www.youtube.com/watch?v=aRVWs1tDarI; https://www.youtube.com/watch?v=m5DZQDzsJsE; https://www.youtube.com/watch?v=g9S4u8eQiww
Lesson 12. Simplifying Expressions with Inverse Trig Functions: https://www.youtube.com/watch?v=Zud3aCeSLRs
Lesson 13. Solving Trigonometric Equations: https://www.youtube.com/watch?v=IE0FxGegdMg; https://www.youtube.com/watch?v=ZkK4ifsQoGk; https://www.youtube.com/watch?v=iZihVtFaAko; https://www.youtube.com/watch?v=kEcbxiLeGTc; https://www.youtube.com/watch?v=YESk2q8QEOY; https://www.youtube.com/watch?v=CrayigBVBZo; https://www.youtube.com/watch?v=IE0FxGegdMg&list=RDQMDgpikCqDgLY; https://www.youtube.com/watch?v=fWI0frnVHy0; https://www.youtube.com/watch?v=7Eo-fuy0f7g; https://www.youtube.com/watch?v=_PPj7eeT_7E
e. Apply polar representations of complex numbers (e.g., DeMoivre's Theorem)
Lesson 14. Polar Representations of CI: https://www.youtube.com/watch?v=fbqakDV-IXc; https://www.youtube.com/watch?v=6HIlT6oSvXc; https://www.youtube.com/watch?v=8RasCV_Lggg; https://www.youtube.com/watch?v=hdlkr0t2R88; https://www.youtube.com/watch?v=u3Q_0WxxdeM
Lesson 15. De Moivre's Theorem: https://www.youtube.com/watch?v=kEf9gt3umnU; https://www.youtube.com/watch?v=yf22lfJ1JCU; https://www.youtube.com/watch?v=y2voZK3-CHA; https://www.youtube.com/watch?v=1Eu66E_MoQ8; https://www.youtube.com/watch?v=irwItP7PiQg
f. Model periodic phenomena with periodic functions
Lesson 16. Modeling: https://www.youtube.com/watch?v=kXKg56CPnpE; https://www.youtube.com/watch?v=RX0DY9eRp8g; https://www.youtube.com/watch?v=s4cLM0l1gd4; https://www.youtube.com/watch?v=6oeBPCzaugI; https://www.youtube.com/watch?v=DP6Drp69fGM; https://www.youtube.com/watch?v=Ogcd_Rhk0bU
g. Recognize equivalent identities, including applications of the half-angle and double-angle formulas for sines and cosines
Lesson 17. Examples: https://www.youtube.com/watch?v=OJz-fOzFbEc; https://www.youtube.com/watch?v=NK4MlZXepYQ; https://www.youtube.com/watch?v=IE8q4WRubC4; https://www.youtube.com/watch?v=d_NMpLSGpkU; https://www.youtube.com/watch?v=A1iKe4HkoXc; https://www.youtube.com/watch?v=uFbbF-IYFjM; https://www.youtube.com/watch?v=qWJ4HwJ_5LY; https://www.youtube.com/watch?v=Wh7hM_FsN3Y; https://www.youtube.com/watch?v=TjWa00qkYpI
Assessment: Practice Problems Problem 1 Problem 2 Problem 3 Problem 4 Problem 5 Problem 6 Problem 7
CSET 3 Math Questions Do Problems 1-5 and 25
Limits and Continuity
a. Derive basic properties of limits and continuity, including the Sum, Difference, Product, Constant Multiple, and Quotient Rules, using the formal definition of a limit
Lesson 18. Definition of a Limit of a Function: https://www.youtube.com/watch?v=-ejyeII0i5c; https://www.youtube.com/watch?v=G0ax2x2_Em0; https://www.youtube.com/watch?v=Fdu5-aNJTzU; https://www.youtube.com/watch?v=0sCttufU-jQ; https://www.youtube.com/watch?v=dXr6aoJ1nVI
Lesson 19. Properties of Limits: https://www.youtube.com/watch?v=lSwsAFgWqR8; https://www.youtube.com/watch?v=6webTCd5gEQ; https://www.youtube.com/watch?v=yzwtrqsvCvI; https://www.youtube.com/watch?v=GGQngIp0YGI; https://www.youtube.com/watch?v=5T8ifCP6eIg; https://www.youtube.com/watch?v=v_Nz6UUQ4HQ; https://www.youtube.com/watch?v=v_Nz6UUQ4HQ
Lesson 20. Infinite Limits: https://www.youtube.com/watch?v=-vwcLvb9A0s; https://www.youtube.com/watch?v=xvFqomOpLrs; https://www.youtube.com/watch?v=tFHALKP22ao
Lesson 21. Limits at Infinity: https://www.youtube.com/watch?v=kae8X6aplf0; https://www.youtube.com/watch?v=FVJNuukADeQ; https://www.youtube.com/watch?v=75xO9xy7TTQ; https://www.youtube.com/watch?v=mrKg_5CsfX0
b. Show that a polynomial function is continuous at a point
Lesson 22. Definition of a Continuous Function: https://www.youtube.com/watch?v=InDHwh1CvOg; https://www.youtube.com/watch?v=kdEQGfeC0SE; https://www.youtube.com/watch?v=oUgDaEwMbiU'; https://www.youtube.com/watch?v=NVQBZWTKygU; https://www.youtube.com/watch?v=SoMl89ZYJIg; https://www.youtube.com/watch?v=OEE5-M4aY4k
Lesson 23. Polynomial function and continuity at a point: https://www.youtube.com/watch?v=OEE5-M4aY4k
c. Apply the intermediate value theorem, using the geometric implications of continuity
Lesson 24. Intermediate Value Theorem and Examples: https://www.youtube.com/watch?v=9xgO-EJ3sr0; https://www.youtube.com/watch?v=9wEHwFrUyOU; https://www.youtube.com/watch?v=TrQTK-B4bzM; https://www.youtube.com/watch?v=Rpug_8nTqyw
Assessment: Practice Problems Problem 1 Problem 2 Problem 3 Problem 4 Problem 5 Problem 6
CSET 3 Math Questions Do Problems 6-9
Derivatives and Applications
a. Derive the rules of differentiation for polynomial, trigonometric, and logarithmic functions using the formal definition of derivative
Lesson 25. Definition of Derivative of a Function: https://www.youtube.com/watch?v=Vv1BUCkgsr8; https://www.youtube.com/watch?v=vzDYOHETFlo
Lesson 26. Differentiation Rules of Algebraic Functions: https://www.youtube.com/watch?v=B2qJURxVyps; https://www.youtube.com/watch?v=v8AmvKHJqTU; https://www.youtube.com/watch?v=hCLfogkqzEk
Lesson 27. Differentiation Rules for Transcendental Functions: https://www.youtube.com/watch?v=TDHI-aieyfk; https://www.youtube.com/watch?v=OjnOgoEu6CM; https://www.youtube.com/watch?v=0YH8BrlVTqk; https://www.youtube.com/watch?v=dylEXVIasqs
Lesson 28. Proofs: https://www.youtube.com/watch?v=JjOndio6-g4; https://www.youtube.com/watch?v=c_CpxQdMejE; https://www.youtube.com/watch?v=ho87DN9wO70; https://www.youtube.com/watch?v=FztF4sJ66rY
Lesson 29. Implicit Differentiation: https://www.youtube.com/watch?v=kk2HilVYAPE; https://www.youtube.com/watch?v=5yTVUZCaU6k; https://www.youtube.com/watch?v=sL6MC-lKOrw; https://www.youtube.com/watch?v=_kLWcuJzYh8; https://www.youtube.com/watch?v=2dv_PfEFZXY
b. Interpret the concept of derivative geometrically, numerically, and analytically (i.e., slope of the tangent, limit of difference quotients, extrema, Newton's method, and instantaneous rate of change)
Lesson 30. Graphing using derivatives: https://www.youtube.com/watch?v=hIgnece9ins; https://www.youtube.com/watch?v=4aYGmexcKnc
Lesson 31. Tangents: https://www.youtube.com/watch?v=1KwW1v__T_0; https://www.youtube.com/watch?v=GH8-URjRQpQ; https://www.youtube.com/watch?v=7EFYoQ6H7Tw
Lesson 32. Newton's Method: https://www.youtube.com/watch?v=1uN8cBGVpfs; https://www.youtube.com/watch?v=HaUKd-UXfMQ; https://www.youtube.com/watch?v=xdLgTDlFwrc
Lesson 33. Instantaneous rate of change: https://www.youtube.com/watch?v=hSK7f4durxI; https://www.youtube.com/watch?v=MRDPyXgxN78; https://www.youtube.com/watch?v=jlihNi_Mkos; https://www.youtube.com/watch?v=4Up5gsDeluw; https://www.youtube.com/watch?v=dPZcJSctp38
c. Interpret both continuous and differentiable functions geometrically and analytically and apply Rolle's theorem, the mean value theorem, and L'Hôpital's rule
Lesson 34. Rolle's Theorem and MVT: https://www.youtube.com/watch?v=0jiVRRKmGoE; https://www.youtube.com/watch?v=jgDykHxQxqM; https://www.youtube.com/watch?v=Du3PuJjME8k; https://www.youtube.com/watch?v=xYOrYLq3fE0; https://www.youtube.com/watch?v=M2b2ok-jto4
Lesson 35. L'Hopital's Rule: https://www.youtube.com/watch?v=PdSzruR5OeE; https://www.youtube.com/watch?v=RQSnbJd04GY; https://www.youtube.com/watch?v=thEnl_gCjXA; https://www.youtube.com/watch?v=Haapl1SrB5I; https://www.youtube.com/watch?v=Zd7wd24jeok; https://www.youtube.com/watch?v=6g_g9-AU188; https://www.youtube.com/watch?v=BU2QhCk3ExY
d. Use the derivative to solve rectilinear motion, related rate, and optimization problems
Lesson 36. Optimization: https://www.youtube.com/watch?v=lzLgtk-lrW0; https://www.youtube.com/watch?v=Zq7g1nc2MJ8; https://www.youtube.com/watch?v=mamH094uw_U; https://www.youtube.com/watch?v=EOJbmMB8uCQ
Lesson 37. Related Rates: https://www.youtube.com/watch?v=BmWmue6sDFg; https://www.youtube.com/watch?v=_kbd6troMgA; https://www.youtube.com/watch?v=kQF9pOqmS0U; https://www.youtube.com/watch?v=kBVDSu7v8os
Lesson 38. Rectilinear Motion: https://www.youtube.com/watch?v=9ot21Up_mj4; https://www.youtube.com/watch?v=HDntI7zfBNs; https://www.youtube.com/watch?v=HzN99FYCg5I; https://www.youtube.com/watch?v=pFeuGMMiZWw
e. Use the derivative to analyze functions and planar curves (e.g., maxima, minima, inflection points, concavity)
Lesson 39. Graphing Functions Using Derivative Concepts: https://www.youtube.com/watch?v=15awMHeP1Yc; https://www.youtube.com/watch?v=pQT2fZRMcf4; https://www.youtube.com/watch?v=3TJLOCYrTes; https://www.youtube.com/watch?v=lDY9JcFaRd4; https://www.youtube.com/watch?v=RoxefQ_Qgm8; https://www.youtube.com/watch?v=kTWXVJHdrwM; https://www.youtube.com/watch?v=Gy9jKk28XHY
Assessment: Practice Problems Problem 1 Problem 2 Problem 3 Problem 4 Problem 5
CSET 3 Math Questions Do Problems 10-15
Integrals and Applications
a. Derive definite integrals of standard algebraic functions using the formal definition of integral and interpret the concept of a definite integral geometrically, numerically, and analytically (e.g., limit of Riemann sums)
Lesson 40. Finding Area using Reimann Sums: https://www.youtube.com/watch?v=AkUa9Fkz2rw; https://www.youtube.com/watch?v=gFpHHTxsDkI; https://www.youtube.com/watch?v=ODwkTt0RMDg; https://www.youtube.com/watch?v=Himr2l8Rd18
Lesson 41. Definite Integral: https://www.youtube.com/watch?v=xR4AnXDBnsw; https://www.youtube.com/watch?v=rCWOdfQ3cwQ; https://www.youtube.com/watch?v=0dDIPzqKgYk; https://www.youtube.com/watch?v=hTTDI49LhjE; https://www.youtube.com/watch?v=8BzIOowS77A; https://www.youtube.com/watch?v=nopnFjMy3rQ
Lesson 42. Properties of Definite Integrals: https://www.youtube.com/watch?v=MM0FTzvedH4; https://www.youtube.com/watch?v=wycadSRDID4
c. Prove the fundamental theorem of calculus, and use it to interpret definite integrals as antiderivatives
Lesson 43. FTC: https://www.youtube.com/watch?v=C7ducZoLKgw; https://www.youtube.com/watch?v=PGmVvIglZx8
Lesson 44: Proof of FTC: https://www.youtube.com/watch?v=pWtt0AvU0KA; https://www.youtube.com/watch?v=mhb0epc6aFk
Lesson 45: Applications of FTC: https://www.youtube.com/watch?v=FcLeaD3UII4; https://www.youtube.com/watch?v=TQTDkpZP02A; https://www.youtube.com/watch?v=lvdnTXZGEF0&list=PL823769CE78CC2EE4
d. Apply the concept of integrals to compute the length of curves and the areas and volumes of geometric figures
Lesson 46: Find length of a curve: https://www.youtube.com/watch?v=neOQXrZv1rY; https://www.youtube.com/watch?v=PwmCZAWeRNE; https://www.youtube.com/watch?v=OhISsmqv4_8; https://www.youtube.com/watch?v=qFowh4Ir7GU; https://www.youtube.com/watch?v=DNDAwWIL5FY
Lesson 47: Area Problems: https://www.youtube.com/watch?v=4bZyfvKazzQ; https://www.youtube.com/watch?v=RebqJ1wqP2I; https://www.youtube.com/watch?v=70NQ3ISYihw; https://www.youtube.com/watch?v=I3bxriE3XbM; https://www.youtube.com/watch?v=B5441_DREY0; https://www.youtube.com/watch?v=LbTH7MGMNjk
Lesson 48: Volume Problems: https://www.youtube.com/watch?v=E5OOMbz5jZk; https://www.youtube.com/watch?v=GJOJl47l2_4; https://www.youtube.com/watch?v=lBSLPUbYFsU; https://www.youtube.com/watch?v=nZqOKc067Z8; https://www.youtube.com/watch?v=R_aqSL-q6_8; https://www.youtube.com/watch?v=43AS7bPUORc; https://www.youtube.com/watch?v=V6nTsxumjgU; https://www.youtube.com/watch?v=cYJRMejnBqI; https://www.youtube.com/watch?v=puSlVA6mwNQ
e. f. Solve separable first-order differential equations and apply them to growth and decay problems
Lesson 49: Examples: https://www.youtube.com/watch?v=nNHlSB6b1HU; https://www.youtube.com/watch?v=6vUjGgI8Dso; https://www.youtube.com/watch?v=DL-ozRGDlkY; https://www.youtube.com/watch?v=XExEixAPK6s; https://www.youtube.com/watch?v=Et4Y41ZNyao; https://www.youtube.com/watch?v=C5-lz0hcqsE; https://www.youtube.com/watch?v=xVWCfMe97ws; https://www.youtube.com/watch?v=9wwaC_jnQQ0; https://www.youtube.com/watch?v=3jpiW_oueaA
Assessment: Practice Problems Problem 1 Problem 2 Problem 3 Problem 4 Problem 5 Problem 6
CSET 3 Math Questions Do Problems 16-20 and 26
Sequences and Series
a. Derive and apply the formulas for the sums of finite arithmetic series and finite and infinite geometric series (e.g., express repeating decimals as a rational number)
Lesson 50: Arithmetic Sum: https://www.youtube.com/watch?v=RM644gFKo_g; https://www.youtube.com/watch?v=Uy_L8tnihDM
Lesson 51: Finite Geometric Series: https://www.youtube.com/watch?v=AXP5PGSaaYk; https://www.youtube.com/watch?v=i8THsl3AYFI
Lesson 52: Infinite Geometric Series: https://www.youtube.com/watch?v=b-7kCymoUpg; https://www.youtube.com/watch?v=yYxzq_O18Mg; https://www.youtube.com/watch?v=x2Xmldq0ll8; https://www.youtube.com/watch?v=ocVBZjuJUdc
Lesson 53: Expressing Repeating Decimals as Rational Numbers: https://www.youtube.com/watch?v=2BgWWsypzLA; https://www.youtube.com/watch?v=7tDK_UjdWOs
b. Determine convergence of a given sequence or series using standard techniques (e.g., ratio, comparison, integral tests)
Lesson 54: Definitions and Examples: https://www.youtube.com/watch?v=FoNLQvf4NUs; https://www.youtube.com/watch?v=lfZGtjSWcQs; https://www.youtube.com/watch?v=muqyereWEh4; https://www.youtube.com/watch?v=NjDk8HiPOhk; https://www.youtube.com/watch?v=7_52IGDHrqY
Lesson 55: Ratio Test - https://www.youtube.com/watch?v=iy8mhbZTY7g; https://www.youtube.com/watch?v=av947KCWf2U; https://www.youtube.com/watch?v=AwJ0P8B25tY; https://www.youtube.com/watch?v=rUis1mSzwyA
Lesson 56: Root Test - https://www.youtube.com/watch?v=vDdDLfIya0I
Lesson 57: Comparison Test - https://www.youtube.com/watch?v=b7OetOcd188; https://www.youtube.com/watch?v=0tXxFPHzFFI; https://www.youtube.com/watch?v=AtbZZiSLemQ; https://www.youtube.com/watch?v=xesQnFWw8f8
Lesson 58: Integral Test - https://www.youtube.com/watch?v=xRyXz_UZ14Q; https://www.youtube.com/watch?v=8jPpNK4GIVs; https://www.youtube.com/watch?v=ojztrQMqLgE; https://www.youtube.com/watch?v=XHUxLLu_c_0; https://www.youtube.com/watch?v=wXDXe9YI4mc; https://www.youtube.com/watch?v=gvZ7UIaC50M
Lesson 59: Divergence Test - https://www.youtube.com/watch?v=1yInzfzDDKY
Lesson 60: Alternating Series Test - https://www.youtube.com/watch?v=91qVGeyTl44
Lesson 61: P Series Test for C or D - https://www.youtube.com/watch?v=w9fC8RaklhA; https://www.youtube.com/watch?v=gvZ7UIaC50M
Lesson 62: Strategies for Testing Series - https://www.youtube.com/watch?v=DvadVYHf3pM; https://www.youtube.com/watch?v=ac00oud9z4A
c. Calculate Taylor series and Taylor polynomials of basic functions
Lesson 63: Taylor and MacLaurin Series - https://www.youtube.com/watch?v=epgwuzzDHsQ&list=PLA5FB0434B1C097D0; https://www.youtube.com/watch?v=cjPoEZ0I5wQ; https://www.youtube.com/watch?v=3d6DsjIBzJ4; https://www.youtube.com/watch?v=Os8OtXFBLkY
Lesson 64: Finding Taylor polynomials of basic functions - https://www.youtube.com/watch?v=epgwuzzDHsQ; https://www.youtube.com/watch?v=19x213y_uk4; https://www.youtube.com/watch?v=8SsC5st4LnI; https://www.youtube.com/watch?v=UINFWG0ErSA
Assessment: Practice Problems Problem 1 Problem 2 Problem 3 Problem 4 Problem 5 Problem 6 Problem 7
CSET 3 Math Questions Do Problems 21-24